I am an enthusiatic but amateurish coder and modeller. Most of the stuff I create services my own immediate research needs, but very occassionally I code something that might be helpful to other people and therefore worth sharing. The best example is a suite of functions created to fit curves to data from relative-timing tasks such as the simultaneity judgement:
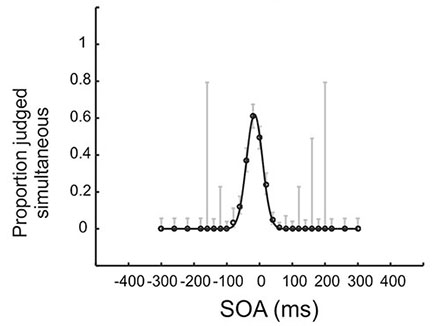
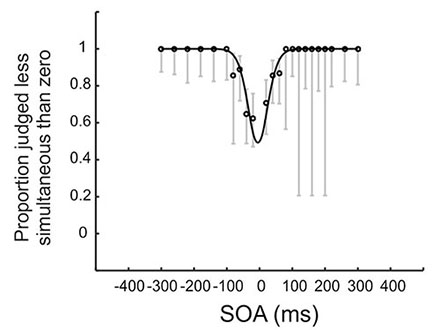

Although there are lots of freeware options out there if you want to fit sigmoidal curves to binary judgements, there are fewer options if you want to fit data from tasks where the likelihood of making one category of judgement (such as "simultaneous") goes up and then comes back down again (or vice versa) as the stimulus changes. In particular, it's hard to find an option that is justified by a formal model of what the observer might be doing.
If you want something like that, most recently I've been working with Bayesian multilevel versions of three different simultaneity judgement models (one that I've worked with a fair bit before, see next section, and a couple of alternatives from other authors). I've been doing this in R, using rstan and stan - all freeware. You can (hopefully) play with these models in the three GUIs (second row of graphs) above. Here's the reference:
- Yarrow, K., Solomon, J.A., Arnold, D.H., Roseboom, W. The best fitting of three contemporary observer models reveals how participants’ strategy influences the window of subjective synchrony. Journal of Experimental Psychology: Human Perception & Performance, 49, 1534-1563 (2023).
You can find the data and code used in this paper here. Feel free to contact me if you want to fit one of these models and need some help.
Alternatively, if you have access to Matlab, and don't fancy working with multilevel models (or want to model a slightly wider range of tasks) try downloading this. These functions implement a model which I've recently been calling GLINC or (most recently) AT-A-GLANCE (Approximation To A Gaussian Latency And Noisy Criteria Equation) for intermodal SJs. They also implement several other models from the same conceptual family, for 2xSJs, TOJs, symmetric (e.g. intramodal) SJs etc. They are fitted (based on maximum likelihood) to each participant separately, so that parameters can be obtained and used in subsequent group-level analyses. There's a readme, and the key functions have a fair bit of text in response to the help command. Further details can be found in these papers (and some older ones which they cite):
- Yarrow, K. Collecting and Interpreting Judgments about Perceived Simultaneity: A Model-Fitting Tutorial. In A. Vatakis, F. Balci, M. Di Luca, Á. Correa (Eds.) Timing and Time Perception: Procedures, Measures, and Applications. Leiden: Brill (2018).
- Yarrow, K., Martin, S.E., Di Costa, S., Solomon, J.A., & Arnold, D.H. A roving dual-presentation simultaneity-judgment task to estimate the point of subjective simultaneity. Frontiers in Psychology, 7:416. (2016)